Onze nieuwste puzzel is eigenlijk heel eenvoudig: in deze grote driehoek staan 46 andere driehoeken. Samen maakt dat zevenenveertig. Toch kan het slechts één op de zeven iets schelen hoeveel driehoeken in deze figuur vervat zitten.
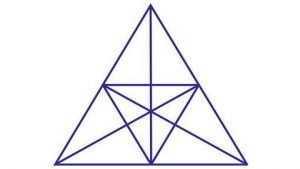
Slechts 14 procent van de puzzelaars die zich op Brilliant.org aan deze puzzel hebben gewaagd, vonden het antwoord belangrijk genoeg om het lange zoeken te rechtvaardigen. Behoor jij tot het selecte groepje dat het ook iets kan schelen?
De oplossing vind je onderaan dit artikel.
Nog even verder scrollen…
Het antwoord is nee. U geeft geen fuck.


Ik ben dol op spelletjes.
Verstandig om niet gelijk het antwoord te geven, want dan denken de mensen niet na.
Nogal een flauwe opgave. Veel te gemakkelijk.
We krijgen een ander verhaal indien we veronderstellen dat de afgebeelde figuur eigenlijk de orthogonale projectie is van een ruimtelijke doorzichtige figuur waarvan enkel de ribben zichtbaar zijn. Centraal bevindt zich een tetraëder met ribbe R, en elk van haar zijvlakken vormt het grondvlak van een piramide. Wat is de hoogte van zo’n piramide opdat de afgebeelde orthogonale projectie correct werd weergegeven?
In het antwoord op deze vraag is slechts 1 op 700000 geïnteresseerd. Ik begin alvast aan het rekenwerk… Komaan, ingenieurkes!
Ik kom dan uit op een hoogte X = R.5.(√6)/12 of: X = 1,02062.R
En gij?
Zeg vriend, op dinsdag moet je niet meer afkomen met de oplossing van de maandagpuzzel, dat is gewoon te laat.
Trouwens, ik ben één van de 699999 anderen.
ik wacht dan wel tot de 10de om mijn antwoord te geven.
Flauwe plezante! Hier dan, als ge me niet gelooft!